Assume-Guarantee Verifier (AGVerifier)
---------------------***---------------------
Author: Hoang-Viet Tran and Pham Ngoc Hung, VNU University of Engineering and Technology.Email:
15028003 "at" vnu "dot" edu "dot" vn
hungpn "at" vnu "dot" edu "dot" vn
---------------------------------------------------------------------------------------------------------
#USER MANUAL
---------------------------------------------------------------------------------------------------------#Required environment:
Our implementation has been tested on the Windows 10 Enterprise, 64 bit.This tool is developed by C#.NET, .NET Framework 4 Client Profile on Visual Studio 2017, the community edition.
#Overview
This is the user manual for the tool AGVerifier version 1.0.0.You can download the installation file here.
Technical report of the tool is available here.
For any information related to the source code or test data, please contact the author.
#Input of this tool
This tool implemented the two assumption generation methods+ The first one uses CDNF algorithm [1] and the proposed algorithms in [2].
+ The second one uses our improved ones which are bases on CDNF and proposed algorithms in [2].
The input file for the assumption generation functions ("Original CDNF" and "Improved CDNF") should have the following format (format 1):
The input file must have 9 lines in the following order:
1. Initial formula for M0.
2. Transition formula for M0.
3. From bool var list for M0.
4. To bool var list for M0.
5. Initial formula for M1.
6. Transition formula for M1.
7. From bool var list for M1.
8. To bool var list for M1.
9. The state predicate (pi).
The input file for the assumption generation functions ("Original CDNF for Evolved M1" and "Improved CDNF for Evolved M1" ) should have the following format (format 2):
The input file must have 11 lines in the following order:
1. Initial formula for M0.
2. Transition formula for M0.
3. From bool var list for M0.
4. To bool var list for M0.
5. Initial formula for M1.
6. Transition formula for M1.
7. From bool var list for M1.
8. To bool var list for M1.
9. The state predicate (pi).
10. Initial formula for the evolved M1.
11. Transition formula for the evolved M1.
#Install this tool
Simply download and run the installer here and follow the instruction of the installation wizard.Note: The installer already contains the test data used during our research. You can use it as initial sample to run the tool.
#Using this tool
The main screenAfter installation, run the AGVerifier tool, the main screen looks like this:
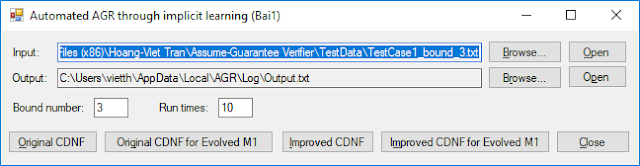
#Generate assumption
In order to generate assumption, please choose a file with format 1 described above for the "Input" and the output file.If you want to generate using the original algorithm, please click on "Original CDNF" button.
If you want to generate using the improved algorithm, please click on "Improved CDNF" button.
After finish processing, you can open the output file for result.
#Generate assumption for the system with evolved M1
In order to generate assumption, please choose a file with format 2 described above for the "Input" and the output file.If you want to generate using the original algorithm, please click on "Original CDNF for Evolved M1" button.
If you want to generate using the improved algorithm, please click on "Improved CDNF for Evolved M1" button.
After finish processing, you can open the output file for result. Please note that in this case, the output file will contain information of both of the process to generate assumption and regenerate the assumption when M1 evolved.
#REFERENCES
[1] N. H. Bshouty. Exact learning boolean functions via the monotone theory. INFORMATION AND COMPUTATION, 123:146–153, 1995.[2] Y.-F. Chen, E. Clarke, A. Farzan, M.-H. Tsai, Y.-K. Tsay, and B.-Y. Wang. Automated assume-guarantee reasoning through implicit learning. In T. Touili, B. Cook, and P. Jackson, editors, Computer Aided Verification, volume 6174 of Lecture Notes in Computer Science, pages 511–526. Springer Berlin Heidelberg, 2010.